Transforming into a Bioinformatician: October 2012

COPASI is an open source modelling and simulation package for biochemical networks, capable of simulation based on ODEs and stochastic kinetics, and models can include discrete events.

A phase space diagram is a type of plots used to describe models that have complex dynamics. The axes represent the variables of the system, and each point in this space represents a state of the system. A trajectory in the phase-space is a line of points that describe the evolution of the state of the system, however time is not explicitly represented in such plots (even though it is implicit).

If the model has two variables, plotting them against each other is an obvious task. What if the model has three variables, like a model of calcium oscillations? At this time, COPASI can only display 2D plots. One solution is to display 2D projections of the phase space. For a model with 3 variables there are 3 possible projections: a vs b, a vs c and b vs c.

To create a phase space model, first download a model. In this case it is described in SBML. COPASI has an option for importing SBML: File -> Import SBML. COPASI may generate some warnings. In the left panel one can see the 3 species and 8 reactions included in the model.

To create a phase-space diagram locate Output Specifications -> Plots down in the left panel. In the Plots panel on the right click new, and a plot with a default name is created.

Double-click the plot in the panel. Now you can give it a meaningful name, and then click New curve. This is where you select the axis of the plot. In this diagram, transient concentrations of species will be plotted. Select a for X axis and b for Y axis and click OK.

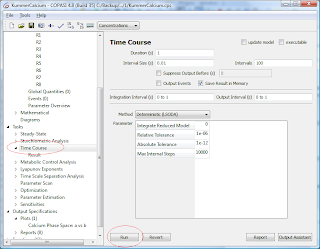
Now a 2D curve appears in the right panel. Parameters can be edited to make them more intuitively understandable. Then, click Commit and select Tasks -> Time Course in the left panel. In the Time Course panel, click Run.