Probability is defined as a chance that a certain outcome will occur. In simple terms, it can be described as the chance, likelihood or odds of some event happening. Probability is measured as the number between zero and one. Zero is absolute certainty that the event will not happen, so it can be said that the probability of the Sun rising in the west is zero. One is the opposite, absolute certainty that the event will happen, such as the Sun rising in the morning. Probability can be written down as a number or a percentage. So the probability of tails when flipping a fair coin is either 0.5 or 50%. In mathematical notation, a random variable that describes a coin toss is defined as (1).
Random variablesA random variable is an important concept in probability. A random variable maps the probability space to a measurable space, therefore it is a function. Each argument, which is a real number, is mapped to an outcome. There are two types of random variables: discrete and continuous. A discrete random variable has a countable amount of possible values, such as the number of times a coin turns up heads or the number of accidents at an intersection during a year. A continuous random variable has an infinite number of possible values, such as the length of a phone call. Even though it can be measured, the precision might be to a millionth of a second and the number of possible lengths is so large that it cannot realistically be counted. Random variables are used when describing probability models. In mathematical notation, a random variable that describes a coin toss is defined as (1).
Probability density functionEach random variable has an associated probability distribution. For a discrete random variable this distribution is called the probability mass function (pmf) and for the continuous random variable – the probability distribution function (pdf). In simple terms, it can be described as the shape of the distribution. It tells how densely or tightly the probability is packed for any point x. The key property of all probability distributions is that the total area under the pdf curve is always equal to one. To understand why, consider that the pdf represents the entire sample space and the event is guaranteed to happen somewhere in that space. Therefore the total probability over the sample space is one. The area below the pdf function to the left of the value x is equal to the probability of the random variable being less than the given x. As an example of the pdf consider the plot generated by the following R script:
x=seq(-4,4,length=200) y=dnorm(x) plot(x,y,type="l", lwd=2, col="blue") x=seq(-1,1,length=100) y=dnorm(x) polygon(c(-1,x,1),c(0,y,0),col="gray")
The script above generates the following plot and the probability that random variable x takes the value between -1 and 1 is equal to the greyed area under the curve.
Figure 1 - An example of probability distribution
From the mathematical perspective, to find the area under the curve over a range the pdf is integrated over that range. Equation (2) calculates the probability of the random variable x being between values a and b.
Cumulative distribution functionCumulative distribution function (cdf) is the total probability of a random variable taking a value less than x. It is useful for finding probabilities of being less than, greater than or between two values of x.
Probability modelsProbability models are used when it is necessary to describe a large number of individual events, where each event follows the same pattern, for example how long a phone call to a call centre is likely to last or how tall a specimen of a certain species is likely to grow. Probability models provide the formulas to describe probabilities.
Uniform random variable and distribution modelA uniform random variable is defined when an event is equally likely to happen on any given value in a finite interval (a, b). For example, when looking for a short in a 1m long piece of a wire, the probability to find it in the first or last 10cm is the same, and equals to 0.1 or 10%. The pdf for the random variable that has uniform distribution can be defined as (3).
The uniform distribution is the most basic continuous random variable: all the values of a probability density function are the same, which means that the occurrence of a random variable within an interval of fixed length is independent of the location of the interval. It is also known as a rectangular distribution, because the area under the curve of the pdf is rectangular in shape, and the pdf itself is a straight horizontal line. Real-life examples may include composition samples from perfect mixtures, arrival times of requests on a web server or just a random number generator. An example of discrete uniform distribution model can be demonstrated by plotting the results of a simple 6-sided die roll, using the following R script:
numcases <- 10000 #number of rolls min <- 1 #minimum and maximum values max <- 6 x <- as.integer(runif(numcases,min,max+1) ) par(mfrow=c(2,1)) hist(x,main=paste( numcases," rolls of a single die"),breaks=seq(min-.5,max+.5,1))
Figure 2 - Uniform distribution model
Exponential distribution modelAnother model of a continuous distribution is the exponential distribution. The exponential distribution has its name because its pdf has the shape of the exponential function. It crosses the Y-axis at some positive value called λ and then slope down to the right in a curve, decreasing towards zero as the values of random variable X increase, but never reaches zero. The amount of slope in the curve is determined by the value of λ. The exponential random variable has the pdf defined in (4).
The cdf for the exponential distribution is defined in (5).
An example of the exponential distribution is plotted using the R script below, using λ=2. The greyed area corresponds to the probability of x taking the value less than 1.
x=seq(0,4,length=200) y=dexp(x,rate=2) plot(x,y,type="l",lwd=2,col="red",ylab="p") x=seq(0,1,length=200) y=dexp(x,rate=2) polygon(c(0,x,1),c(0,y,0),col="lightgray")
Figure 3 - Exponential distribution model
The exponential distribution can be applied to describe a number of various processes. The amount of time from now until the next earthquake occurs has an exponential distribution. It also describes the length of phone calls or the amount of time the battery lasts. The amount of change in someone’s pocket or the amounts of money customers spend in the supermarket also follow an exponential distribution. It is intuitively easy to visualize, because most customers would spend a relatively small amount of money, only a small percentage would spend over $200 in one visit, and very rarely someone would spend over a thousand. Hence the probability will be highest for small amounts, and will approach zero for large amounts.
An important property of the exponential random variable is memorylessness. If X represents a waiting time, then the probability of waiting a given length of time is not affected by the time waited already. This is described by a formula
In other words, if you have already waited a minutes, the probability of waiting another b minutes is the same as the initial probability of waiting b minutes.
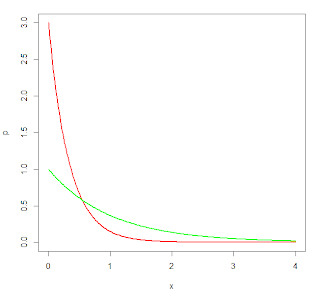
The constant λ is the reciprocal of the mean of the exponential distribution. So, if the value of λ is large, the distribution has a small mean and quickly drops toward zero. If the value of λ is small, the mean is large and the distribution drops very slowly. This is illustrated by the following R script, which plots the distribution with λ=3 in red and λ=1 in green. The red curve drops towards the zero much faster than the green one.
x=seq(0,4,length=200) y=dexp(x,rate=3) x1=seq(0,4,length=200) y1=dexp(x1,rate=1) plot(x,y,type="l",lwd=2,col="red",ylab="p") lines(x1,y1,type="l",lwd=2,col="green",ylab="p")
Figure 4 - Influence of λ on exponential distribution
The expected value of an exponential distribution is equal to 1/λ.
An example of applying the properties of the exponential distribution to a problem:
Suppose that the amount a person waits in line has a mean of 10 minutes, exponentially distributed with λ=1/10. What is the probability that a person will spend more than 15 minutes in a line? What is the probability that a person will spend more than 15 minutes in a line, if he is still in a line after 10 minutes?
Answer:
Exponential random variates can be generated from the uniform random variates according to (7).
To visually confirm this property of the exponential distribution, the following R script first generates uniform random variates and then applies (7) to each of them to calculate the value of x, which is then plotted on the graph in Figure 4.
n<-100
lambda <- 1
UnifRandVar <- runif(n, min=0, max=100)
ExpRandVar <- -(1/lambda)*log(UnifRandVar)
plot(UnifRandVar, ExpRandVar, col="blue", xlab="Uniform Random Variates", ylab="Exponential Random Variates", main=paste("Plot of ", length(UnifRandVar), " exponential variates given lambda=", lambda), col.main="red")Figure 5 - Exponential variates generated from uniform variable
References:
Aitken M, Broadhurst B, Hladky S, Mathematics for Biological Scientists 2010, Garland Science, NY and LondonGraham A, Statistics: An Introduction 1995, Hodder & Stoughton Educational, London, UK
Press W, Teukolsky S, Vetterling W, Flannery B, Numerical Recipes: The Art of Scientific Computing, 3rd edition 2007, Cambridge University Press, UK
Rumsey D, Probability for Dummies 2006, Wiley Publishing, Hoboken, NJ, USA.
Mathematics for Metabolic Modelling - Course Materials 2012, University of Manchester, UK
by Evgeny. Also posted on my website










Random variable stochiametric problems are solved by these concepts which are given here.There are different formulas to solve these questions.
ReplyDeleteProbability Distribution Function