Introduction
The network that I have been using is a generalised view of the interactions that may take place. By adding gene expression data to the network, I will be able to determine which interactions are 'active' under the known experimental conditions. The data provided for analysis was from an experiment to examine the changes in gene expression in the lungs of rats exposed to mustard gas (GSE1888).
The goal was to find, identify and compare the active modules and how they overlap with the network of proteins affected by mustard gas.
1. Functional Modules
When the protein interactions are represented as graphs, they can be used to investigate the functions of proteins through their interactions with neighbouring proteins. Clusters of highly interconnected proteins could not have occurred by chance and are likely to contain proteins with a common biological function (Dunn et al, 2005). Such clusters are called functional modules and their identification is a complex task.
Bader and Hogue (2003) suggested the three-stage algorithm for finding molecular complexes. The algorithm assigns weights to nodes based on “cliquishness” of a node, which is proportional to the number of nodes in the neighbourhood and inversely proportional to the vertex size of the neighbourhood.
Dunn et al. (2005) note that in certain cases, such as a prey node attached to the bait by a single edge, a poorly connected node provides useful information. Methods that use edge-betweenness, unlike many other clustering methods, will not remove such nodes and are useful when the information associated with these low degree nodes is required.
2. Finding Active Modules
The file provided for the exercise contained significance values of the difference in gene expression in rats that were exposed to 6mg/kg mustard gas for 1, 3 and 6 hours. The jActiveModules plugin was used to find active modules. The plugin identified five functional modules ranging from 69 to 95 nodes in size.

3. Examining Active Modules
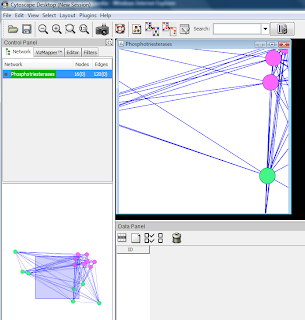
Network from module 1.1 hour: all significance values are equal to 0.999783355
3 hours: significance values in range of 4.5*10-5 to 0.489861449

Graphical view, with nodes having higher significance values coloured with darker red.

In this network, only five proteins have significance values over 0.01.
6 hours: significance values in range of 6.13*10-8 to 0.916047284

This time, over 30 proteins have significance values over 0.01.
Network from module 2.1 hour: all significance values are equal to 0.999783355
3 hours: significance values in range of 4.5*10-5 to 0.489861449

6 hours: significance values in range of 6.13*10-8 to 0.916047284

4. Comparing the Modules Identified
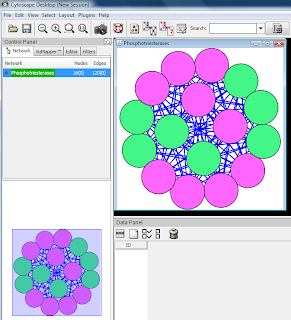
After networks were created from first three of the five active modules identified, the Cytoscape plugin Advanced Network Merge was used to merge these three modules.

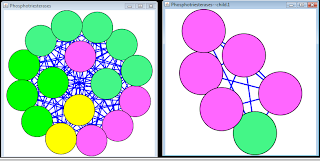
The merged network which is coloured according to the differential expression at 6 hours was represented on the image below:

It is not immediately obvious from the picture how strongly the three networks which were merged into one overlap. One observation is that the merged network has 118 nodes, while the three child networks would have 95 + 44 + 72 = 211 nodes if there was no overlap. This is an indication that a significant number of nodes are present in two or three child networks.
Another approach may be to compare the proteins with high p-values. To fill the table below, the nodes in each of the child active modules were sorted by p-value at 6 hours. Then ten proteins with highest p-values were inserted into the table. One protein (Icam1) was present in all three “top tens”. Module 1 and 2 share one other protein (Krt19), and modules 1 and 3 share one other protein (Lpl), while modules 2 and 3 share five other proteins (Cd36, Hamp, Sacm11, Tim3, Dusp1). From this basic analysis it can be roughly estimated that all three modules are overlapped to some extent, and modules 2 and 3 are more significantly overlapped compared to module 1 and 2 or 1 and 3. Further more detailed analysis is required to make more exact conclusions.
| Active Module 1 | Active Module 2 | Active Module 3 |
|---|---|---|
| Lpl | Lpl | |
| Sele | ||
| Icam1 | Icam1 | Icam1 |
| Il18 | ||
| Krt19 | Krt19 | |
| Nr1h3 | ||
| Pla2g1b | ||
| Col5a2 | ||
| Nt5e | ||
| Pawr | ||
| Axin1 | ||
| Cd36 | Cd36 | |
| Hamp | Hamp | |
| Sacm1l | Sacm1l | |
| Timp3 | Timp3 | |
| Mark3 | ||
| Dusp1 | Dusp1 | |
| Phlda1 | ||
| Pcm1 | ||
| Raf1 | ||
| Gsk3b |
References:
R. Dunn, F. Dudbridge, C. Sanderson, The Use of Edge-Betweenness Clustering to Investigate Biological Function in Protein Interaction Networks, BMC Bioinformatics, 6:39 (2005)
G. Bader, C. Hogue, An automated method for finding molecular complexes in large protein interaction networks, BMC Bioinformatics, 4:2 (2003)
Feedback
You have identified and shaded active modules. However, it is more interesting at this stage to shade by fold change, rather than by significance value. By using the fold change values (1hexp, 3hexp, 6hexp) you can see which parts of your network are up/down-regulated over the course of the experiment. In the practical instructions I suggested that you use the intersection option when merging your networks. This does show you the extent of the overlap.
My Comment
It was quite stupid of me to use 'union' instead of 'intersect' when merging networks and then record that there are no obvious observations.
by Evgeny. Also posted on my website